题解 P2898 【[USACO08JAN]haybale猜测Haybale Guessing】

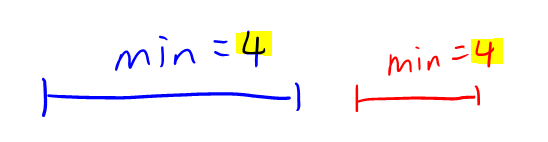
简要题意：小母牛回答你 $q$ 次区间 $[l,r]$ 上的最小值，判断最早哪个句子会出现矛盾。 这题有点米奇妙妙屋。 先来思考简单的情况，知道两个区间的最小值，如何判定矛盾？ 显然这种情况是矛盾的：  然而这道题还有一个条件，序列上每个位置 $a_i$ 不同，所以这种情况也不可能发生：  还有一种 $l_2$ 只有一个端点 $\in$ $l_1$ 的情况——区间有交集，但不是完全覆盖 $\Rightarrow$ 区间最小值可以不一样也可以一样。 整理一下： - 两区间**无交集**，他们的最小值不应该相同。 - 一个区间**被**大区间**完全覆盖**，它的最小值只能大于等于大区间最小值。 也就是说这道题的判定转化为了一个区间覆盖的判定问题，是否出现矛盾我们通过区间覆盖的关系来求。 我们将区间最小值从大往小排序，这样的话如果一个区间最小值比较小，但它被大区间覆盖了（相应地 这个大区间的最小值比它大，排在前面），这个时候就不对劲；如果枚举到几个区间最小值相同，但他们互不相干，也能推导出矛盾关系。所以这样处理就变成了区间覆盖问题。  好啦我会做啦！把 $1$ 到 $q$ 的回答按 $val$ 排序，再记一个回答的编号 `q[i].id` 搞搞，这样就能知道啥时候有矛盾了！ naive! 这道题求的是最早的矛盾出现时间，如果排序后一个 $id=4$ 的区间被 $id=5$ 的区间覆盖且出现了矛盾，能说明最早的矛盾在 $4$ 吗？不能。这个时候我们只能知道在这个时间段有矛盾，但是没法定位最早的矛盾。又因为在 $1-k$ 的句子中没有矛盾，$1-k'(k'\le k)$ 中肯定也没有矛盾，这个问题实际上是有单调性的。问题只会出现在 没有问题的时间 之后，所以可以二分这个时间 $k$，如果没矛盾那么二分后面的，出现矛盾则往前二分。 区间覆盖可以用线段树区间 set 来做。这个区间能被完整查询到则说明被覆盖了。如果有 $val$ 相同的我们更新一下交集和并集，都有交集的话那肯定没事了，然后把这些段的并集 update 到树上。这个时候它们的并集肯定是一段完整的区间段的，因为有一个区间和前面的 $val$ 相同的没交集就出错了。要是没有 $val$ 相同的我们就判断一下 $q_i$ 这个区间段能不能被查到，更新就更新它这一段就好了。 我感觉应该讲的比较详细了，结合代码看看应该比较好懂。 ```cpp const int inf = 1000000000; inline int read() { register int x = 0, c = getchar(); bool f = 1; for(; !isdigit(c); c = getchar()) f ^= c == '-'; for(; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48); return f ? x : -x; } struct A { int l, r, mn; inline bool operator<(const A &rhs) const { return mn == rhs.mn ? l < rhs.l : mn > rhs.mn; // 按 val 排序 } } a[MAXN], b[MAXN]; int n, m; struct Node { int sum, tag; } tr[MAXN * 4]; #define ls(p) p << 1 #define rs(p) p << 1 | 1 inline void maintain(int p, int l, int r, int v) { tr[p].sum = (r - l + 1) * v; tr[p].tag = v; // segtree 区间set } inline void pushDw(int p, int l, int r) { int mid = (l + r) >> 1; maintain(ls(p), l, mid, tr[p].tag); maintain(rs(p), mid + 1, r, tr[p].tag); tr[p].tag = 0; } void update(int p, int l, int r, int ql, int qr, int v) { if(ql > qr) return; if(ql <= l && r <= qr) return maintain(p, l, r, v); if(tr[p].tag) pushDw(p, l, r); int mid = (l + r) >> 1; if(ql <= mid) update(ls(p), l, mid, ql, qr, v); if(qr > mid) update(rs(p), mid + 1, r, ql, qr, v); tr[p].sum = tr[ls(p)].sum + tr[rs(p)].sum; } int query(int p, int l, int r, int ql, int qr) { if(ql > qr) return 0; if(ql <= l && r <= qr) return tr[p].sum; if(tr[p].tag) pushDw(p, l, r); int mid = (l + r) >> 1, ret = 0; if(ql <= mid) ret += query(ls(p), l, mid, ql, qr); if(qr > mid) ret += query(rs(p), mid + 1, r, ql, qr); return ret; } inline bool chk(int x) { memset(tr, 0, sizeof tr); for(int i = 1; i <= x; ++i) b[i] = a[i]; sort(b + 1, b + x + 1); int ul, ur, nl, nr; for(int i = 1; i <= x;) { int j = i; while(j <= x && b[j].mn == b[i].mn) ++j; ul = nl = b[i].l, ur = nr = b[i].r; // ul ur 并集；nl nr 交集 for(int k = i + 1; k < j; ++k) { // 如果j=i开始往后扫 最后i=j更新i的话，注意循环范围 ul = min(b[k].l, ul); ur = max(b[k].r, ur); nl = max(b[k].l, nl); nr = min(b[k].r, nr); } if(nl > nr) return 0; if(query(1, 1, n, nl, nr) == nr - nl + 1) return 0; update(1, 1, n, ul, ur, 1); // 如果没有相同的这样写就相当于 bi.l bi.r i = j; } return 1; } int main(void) { n = read(), m = read(); for(int i = 1; i <= m; ++i) a[i].l = read(), a[i].r = read(), a[i].mn = read(); int l = 1, r = m + 1; while(l < r) { int mid = (l + r) >> 1; if(chk(mid)) l = mid + 1; else r = mid; } printf("%d\n", l == m + 1 ? 0 : l); // 注意这里，这种二分写法 (l + r) / 2 是取不到 r 的，但是这里 r=m 是可以成为答案的 // 所以这种写法需要由原来的 [1,x] 扩展到 [1,x+1]，x 为 r 的取值点 return 0; } ```